March 18, 2025 (Updated on: March 18, 2025)

Convergence of the perimeter of an inscribed regular polygon

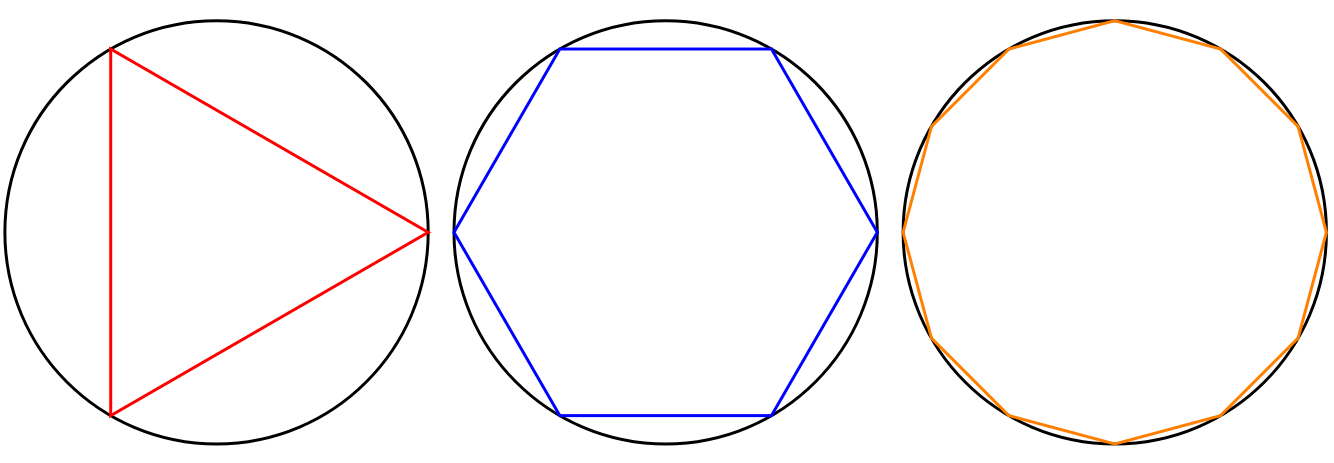
If you draw a triangle inside a circle, its perimeter is much shorter than the circle’s circumference. But as you add more sides, the polygon starts hugging the circle. Intuitively, with infinitely many sides, its perimeter should match the circle’s circumference, isn't it ? Well, let’s prove it.

Consider a $n$-sided regular polygon inscribed in a circle of radius $r$. The summits of the polygon lie on the circle, and all sides of the polygon are of equal length.
The angle at the center of a regular polygon is the angle formed by two consecutive rays of the circle passing through the vertices of the polygon. Since the polygon is regular, all these angles at the center are equal.

• Full circle circumference : The complete circumference of a circle is $2\pi$ radians.
• Number of sides: The polygon has $n$ sides.
• Circumference division: Each side of the polygon subtends an angle at the center that is a fraction of the total circumference. Since the polygon has $n$ sides, the circumference is divided into $n$ equal parts.

Therefore, the centrale angle subtended by a side of the polygon is :

$$\text{Central angle} = \frac{2\pi}{n} \text{ radians}$$

Example : For $n = 6$ (hexagon), each side subtends an angle at the center of : $\frac{2\pi}{6} = \frac{\pi}{3} \text{ radians}$

Thanks to the inscribed angle theorem , we know that :

$$\text{Base angle} = \frac{\text{Central angle}}{2} = \frac{\pi}{n}$$

Let’s take the isosceles triangle $OAB$ where :

• $O$ is the center of the circle.
• $A$ and $B$ are two consecutive vertices of the polygon.
• $OA$ and $OB$ are the radii of the circle, each of length $r$.
• $AB$ is a side of the polygon, of length $s$.

We have proved that :

• The centrale angle $\angle AOB = \frac{2\pi}{n}$
• And that every angle at the base $\angle OAB$ et $\angle OBA$ is $\frac{\pi}{n}$

To find the length of side $s$, we can use trigonometry in the $OAB$ triangle ; the definition of sine is : $\sin(\frac{\pi}{n}) = \frac{\text{opposed}}{\text{hypoténuse}}$

And as :

• The hypotenuse is the radius $OA$, which is $r$.
• The opposite side is half the side $AB$, which is $\frac{s}{2}$.

Then we have :

$$\sin\left(\frac{\pi}{n}\right) = \frac{s/2}{r}$$ $$\frac{s}{2} = r \sin\left(\frac{\pi}{n}\right)$$

Thus, the length of a side $s$ of the regular polygon inscribed in a circle of radius $r$ is given by :

$$s = 2r \sin\left(\frac{\pi}{n}\right)$$

We now have all we need to demonstrate the value of the perimeter of a polygon.

The perimeter $P$ of the polygon is the sum of the lengths of all its sides. Since the polygon has $n$ sides, each of length $s$, the perimeter is :

$$P = n \cdot s = n \cdot 2r \sin\left(\frac{\pi}{n}\right)$$

The basic question was to find out the value of the perimeter $P$ of the inscribed regular polygon when the number of its sides $n$ tends towards infinity.

$$\lim\limits_{n \to \infty} P = 2\pi r$$

We know that for small angles $\sin{x}=x$ and when $n$ is very large, $\frac{\pi}{n}$ is small. We can therefore use this approximation :

$$\sin\left(\frac{\pi}{n}\right) \approx \frac{\pi}{n}$$

Substituting this approximation into the perimeter expression, we obtain :

$$P \approx n \cdot 2r \cdot \frac{\pi}{n} = 2\pi r$$

Thus, when $n$ tends to infinity, the perimeter $P$ of the regular polygon inscribed in the circle tends to $2\pi r$, which is the circumference of the circle:

$$\lim\limits_{n \to \infty} P = 2\pi r$$